とっても便利!【暗算の秘訣】とは?
みなさん、掛け算の九九ってどうやって覚えましたか?
「インイチが1、インニが2…」と、まるで呪文のように1の段からひたすら唱えてた記憶、ありませんか?
今の小学生は「九九の歌」でリズムにのせて楽しく授業で覚えてるみたいです。更に最近では「インド式かけ算」というのがあって、小学生でも(19×19)まで暗算できる子もいるとか…、なんだか時代を感じます。
とっても便利な「①インド式かけ算」と「②ゾロ目のかけ算」をご紹介!
①十の位が同じ2ケタの数どうしのかけ算
たとえば…
18×16、21×28、38×39、41×48、55×59、67×66、77×71、89×87、99×99 など
これが暗算で出来れば、かなり便利!
【解き方】
例)11×16=288 まず、暗算で計算する為に掛け算を2つ作成。
1つ目のかけ算
最初の数の二桁の数字(18)と次の数(16)の一桁の数字(6)に注目
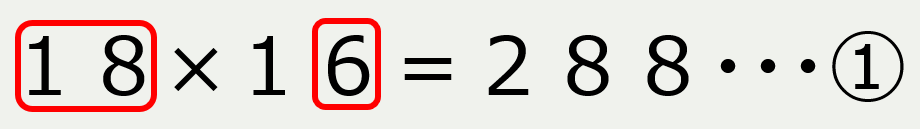
次の数の一桁目の数字(6)を最初の数の二桁の数字(18)に移動してプラス。
次の数は一桁目の数字(6)が無くなったので、(6)をマイナス。
すると計算式が、24×10=240 となり、これが1つ目の掛け算。

2つ目のかけ算
最初の数(18)の一桁の数字(8)と次の数(16)の一桁の数字(6)を掛ける

②と③を足したのが答え①! スゴイ!
【実践編】
一見、難しそうな計算もコレを使えば簡単に!
例)3,200万円の38%は? 3,200万円×0.38=32万円×38 となるので…
40万円×30=1,200万円…②
2万円×8=16万円…③
1,200万円+16万円=1,216万円…②+③
②ゾロ目と足したら10になる時の二桁のかけ算
たとえば…
77×64、55×28、33×19、11×46、22×55、66×37、44×73、88×82、99×19 など
使う頻度は少ないけど、これも便利!
【解き方】
例)77×64=4,928 まず、暗算で計算する為に掛け算を2つ作成。
1つ目のかけ算
最初の数(77)の十の位と次の数(64)の十の位の数字(7)と(6)に注目
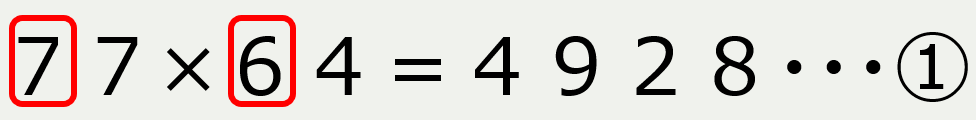
どちらかの十の位の数字に「1」を足して掛けた答えが最初の二桁になる
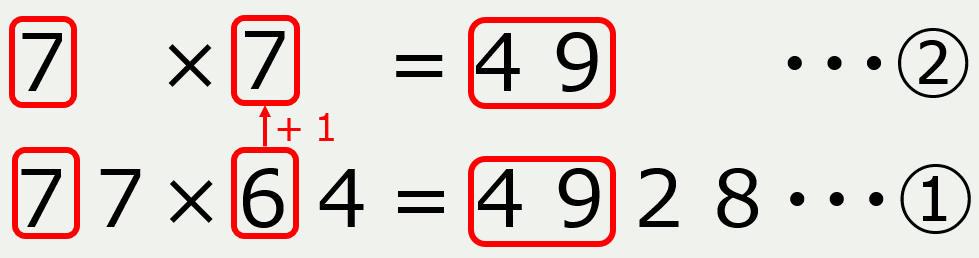
2つ目のかけ算
最初の数(77)の一の位と次の数(64)の一の位の数字(7)と(4)に注目
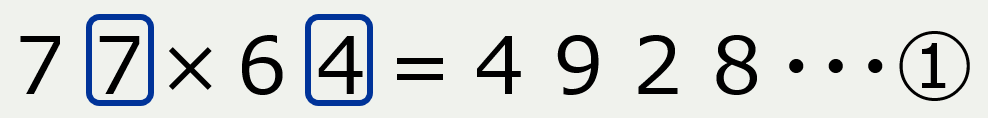
最初の数の一の位の数字(7)と次の数の一の位の数字(4)を掛けた答えが残りの二桁
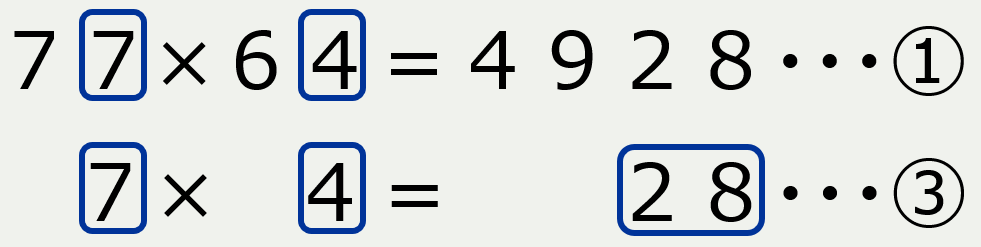
②と③を足したのが答え①! スゴイ!
まとめ
この二桁の掛け算の暗算テク、実は小学校でも大活躍なんです。
どこで役に立つかというと…そう、6年生で習う「円の面積」の計算!
公式は「半径 × 半径 × 3.14」なので、同じ数を掛ける場面が出てくるんですよね。
たとえば半径が16cmなら、16×16を暗算でパッと出せたら楽チン!
「こんなワザ、小学生のときに知りたかった~⁉」って、思うくらいシンプル!
日常生活でも使えるので、親子で一緒にチャレンジしてはいかがでしょうか♪
